20172318 2018-2019-1 《程序设计与数据结构》第6周学习总结
教材学习内容总结
树
- tree:树 树是一种非线性结构,其元素是按分层组织的。
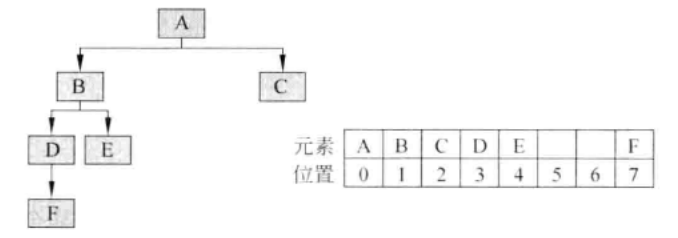
- 一种可能的计算策略是将元素n的左孩子置于位置(2×n+1),将右孩子置于位置(2x(n+1))
- node:结点 树中的一个位置。
- edge:边 树中两个结点的连接。
- root:根结点 位于树中最高层的结点,在该树中,该结点没有父结点。
- level:层结点 相当.于树的根结点的位置。
- child:子结点 位于树中当前结点下面的结点,并由边与之直接连接。
- sibling:同胞结点 属于同一结点的子结点。
- leaf:叶结点 树中不再有任何了结点的结点。
- internalnode:内部结点 树中的结点,它不是根结点,且至少有一个子结点。
- path:路径 连接树中一个结点与另一个结点的边的集合。
- ancestor:祖先结点 位于当前结点以上的结点。
- descendant:后代结点 位于当前结点一下的结点。
- pathlength,路径长度 连接一个结点与另一个结点的边的数量。
- treeheight:树高度 从根结点到叶结点的最长路径的长度。
- 一般而言一棵含有m个元素的平衡n元树具有的高度为lognm
- treeorder:树的阶 树中结点具有的最大子结点数。
- generaltree:一般树 对结点的子结点数没有限制的树。
- n-arytree:n元树 结点的子结点数不多于n的树。
- binarytree:二叉树 结点的子结点数不多于2的树。
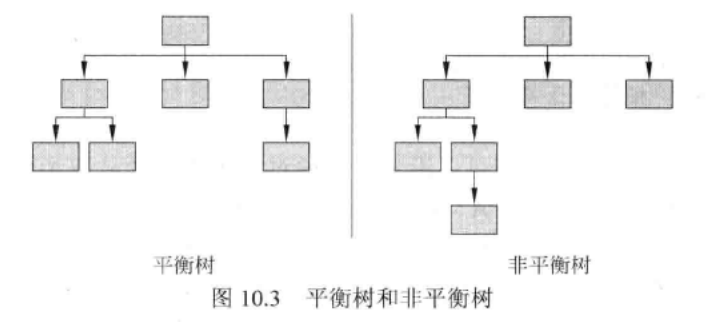
- balanced:平衡 粗略地说,如果所有叶结点都位于同一层,或至少位于其他某一层,就认为是平衡树。
- complete:完全 如果是平衡树,且最底层的叶结点位于树的左边,就认为是完全树。
- full:完整 如果树的所有叶结点位于同一层,且每个结点要么是叶结点,要么正好有n个子结点,那么就认为这种n元树是完整树。
- freelist:在树的数组实现中,可用位置的列表。
- binarysearchtree:二叉查找树 左子结点总是小于父结点,而父结点又总是小于或等于右子结点,那么这种二叉树就是二叉查找树。
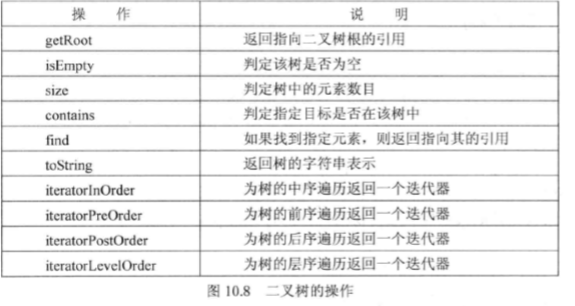
- preordertraversal:前序遍历 从根结点廾始,访问每一结点及其孩了的树遍历。
- inordertraversal:中序遍历 从根结点开始,访问结点的左子结点,再是该结点,然后是其余结点的树遍历。
- postordertraversal:后序遍历 从根结点开始,先访问孩子结点,然后访问每一结点的树遍历。
- level-ordertraversal:层序遍历 从根结点开始,每次访问同一层中的所有结点的树遍历。
- 用链表实现二叉树
- BinaryTreeNode类。该类负责跟踪存储在每个位置上的元素,以及指向每个结点的左右子树或孩子的指针。
- find方法。与前面集合中的一样,find方法通过使用存储在树中的类的equals方法来判定等同性,来遍历该树。这就将等同性的定义置于了存储在树中的那个类的控制之下。如果没有找到目标元素,那么find方法将抛出一个异常。
- iteratorlnOrder方法。其任务是创建一个Iterator对象,它允许一个用户类在中序遍历中单步遍历树的元素。该问题的解决方案给我们提供了使用一个集合来构建另一个集合的另一例子。我们仅仅通过使用前面伪代码中的一个visit定义来遍历该树,该伪代码将结点的内容添加到了某个无序列表中。然后,作为该树的iterator方法的结果,返回该列表迭代器。
教材学习中的问题和解决过程
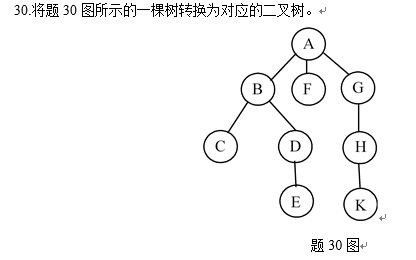
- 问题1:如何将一棵树转化为对应的二叉树?
- 问题1解决方案:
将 节点的孩子 放在左子树;
将 节点的兄弟 放在右子树。

代码调试中的问题和解决过程
无
上周考试错题总结
上周无测试

点评过的同学博客和代码
- 本周结对学习情况
- 课本内容总结有自己的理解,图片较少
- 结对学习内容
- 课本第十章
学习进度条
| 代码行数(新增/累积) | 博客量(新增/累积) | 学习时间(新增/累积) | 重要成长 | |
|---|---|---|---|---|
| 目标 | 5000行 | 30篇 | 400小时 | |
| 第一周 | 0/0 | 1/1 | 8/8 | |
| 第二周 | 500/500 | 1/2 | 15/ 23 | |
| 第三周 | 802/1302 | 1/3 | 12/35 | |
| 第四周 | 1530/2832 | 2/5 | 15/50 | |
| 第五周 | 1165/3997 | 1/6 | 10/60 | |
| 第六周 | 1169/5166 | 1/7 | 15/75 |